

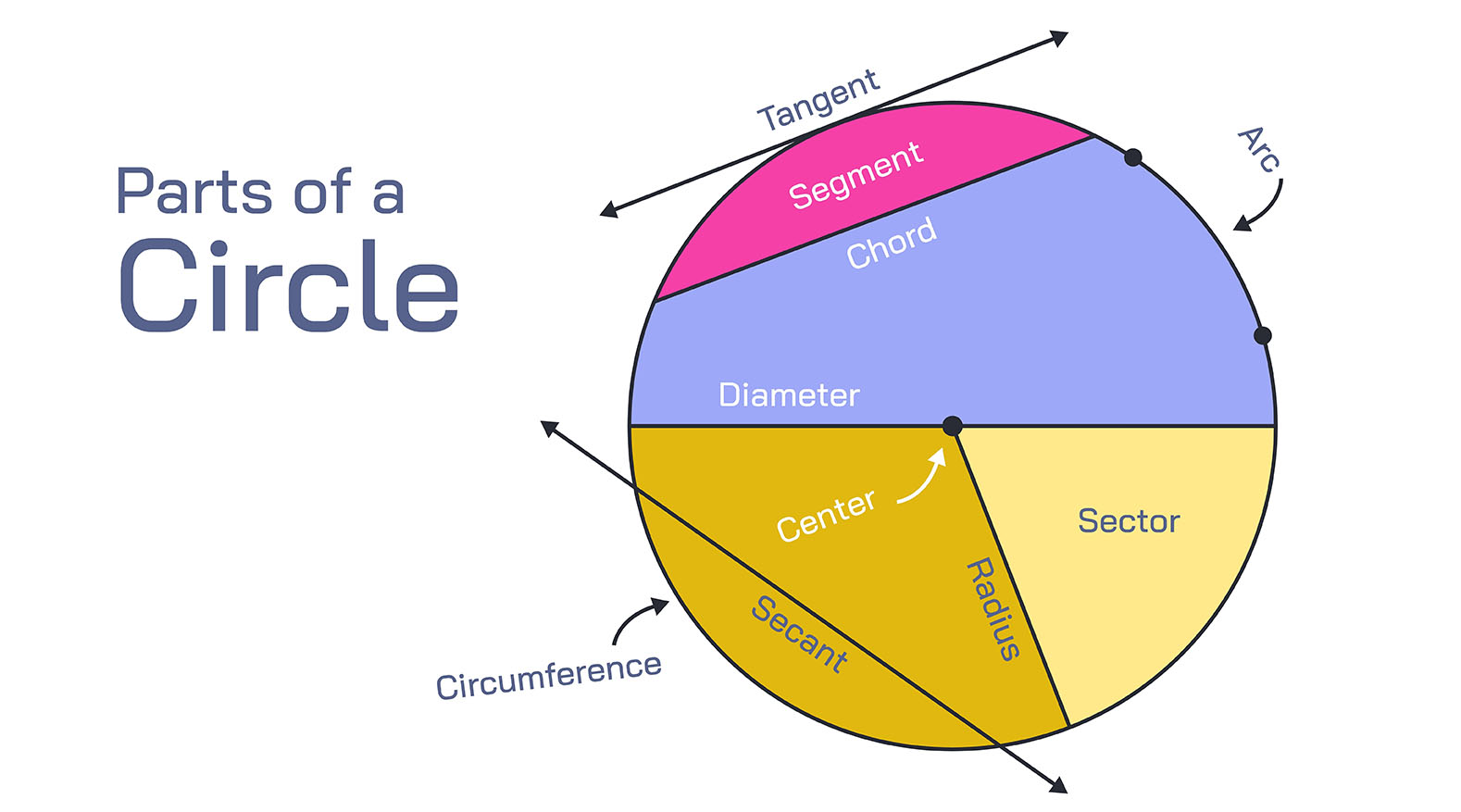
A radius is a line segment that connects the centre of a circle to a point on the circle. The radius is the shortest distance from the centre of the circle to any point on the circle.
The radius of a circle is always half the diameter of the circle. The diameter is the distance across the circle, passing through the centre.
The radius of a circle can be used to calculate the area of the circle. The area of a circle is equal to πr², where π is a mathematical constant that is approximately equal to 3.14 and r is the radius of the circle.
The radius of the sphere is 5 cm.
Noun:
The word "radius" comes from the Latin word "radius", which means "ray".
The first recorded use of the word "radius" in English was in the 14th century.
Why might it be useful to know the radius of a circle?
Question:
Define the term "radius" in the context of geometry and explain its significance in measuring and describing circles.
Answer:
In geometry, the "radius" of a circle is a fundamental measurement that refers to the distance from the centre of the circle to any point on its circumference. It is denoted by the letter "r." The radius is a key property of circles and plays a crucial role in understanding their properties and relationships.
The radius is significant in various ways. First, it determines the size of the circle. The longer the radius, the larger the circle's diameter and circumference. Additionally, the radius helps define the circle's area through the formula A = πr², where "A" represents the circle's area and "π" is a mathematical constant (approximately 3.14159).
Furthermore, the radius aids in measuring distances within the circle. It allows us to calculate the length of arcs and the curvature of circular segments. Moreover, the radius, along with the centre, helps in constructing circles and analyzing their geometric properties.
Address
Developing Experts Limited
Exchange Street Buildings
35-37 Exchange Street
Norwich
NR2 1DP
UK
Phone
01603 273515
Email
hello@developingexperts.com
Copyright 2025 Developing Experts, All rights reserved.