Back
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

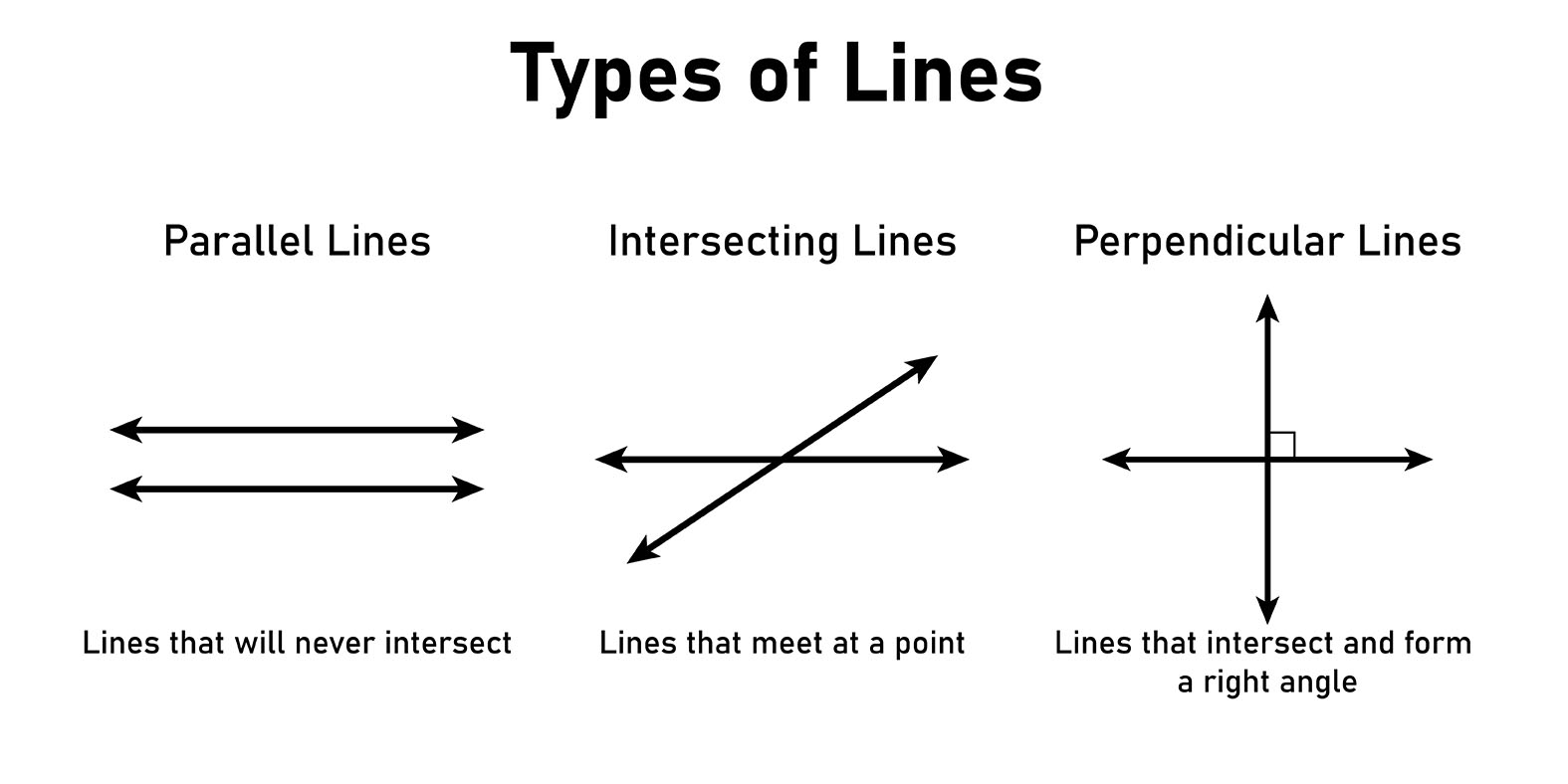
perpendicular

Primary Information
Secondary Information

Definition

Perpendicular lines are lines that intersect at a right angle. This means that the two lines form an angle of exactly 90 degrees.

Perpendicular lines are important in many different areas of mathematics and science. For example, they are used in geometry to construct shapes, in trigonometry to solve problems, and in physics to study motion.

Here is a more formal definition of perpendicular lines:

Two lines are said to be perpendicular if the angle between them is a right angle.

This definition can be used to prove many different theorems about perpendicular lines. For example, it can be used to prove that the opposite angles of a rectangle are congruent.

How can the word be used?

The beam was supported by two perpendicular columns.

perpendicular

Different forms of the word

Adjective:

  • perpendicular (at right angles to something else).
  • perpendicularity (the state of being perpendicular).

Noun:

  • perpendicular (a line or plane that is perpendicular to something else).

Etymology

The word "perpendicular" comes from the Latin word "perpendiculum", which means "plumb line". The first recorded use of the word "perpendicular" in English was in the 14th century.

Question

What does perpendicular mean?

AQA Science Exam Question and Answer

Question:

Explain the concept of perpendicular lines and their significance in geometry and real-world applications. Provide examples of situations where perpendicular lines are essential and describe how they are identified.

Answer:

Perpendicular lines are a fundamental concept in geometry, referring to lines that intersect at a right angle, creating four 90-degree angles. This relationship holds true whether the lines are horizontal and vertical or at different orientations in space. In real-world applications, perpendicular lines play a crucial role in various fields.

One practical example is in construction, where ensuring walls, beams, and supports are perpendicular is essential for stability and structural integrity. Architects and engineers use tools like a carpenter's square or laser levels to establish right angles and ensure accuracy.

In navigation, perpendicular lines are significant when determining bearings and directions. A compass needle, for instance, aligns with Earth's magnetic field, indicating the magnetic north direction, which is perpendicular to the equator.

Perpendicular lines are also crucial in trigonometry, where the concept of slope in right triangles is essential. The slope of a line perpendicular to another line is the negative reciprocal of the original line's slope.

Identifying perpendicular lines often involves using visual aids or tools like a protractor to measure angles. In digital environments, coordinates and equations are used to determine perpendicularity.