fraction
Definition
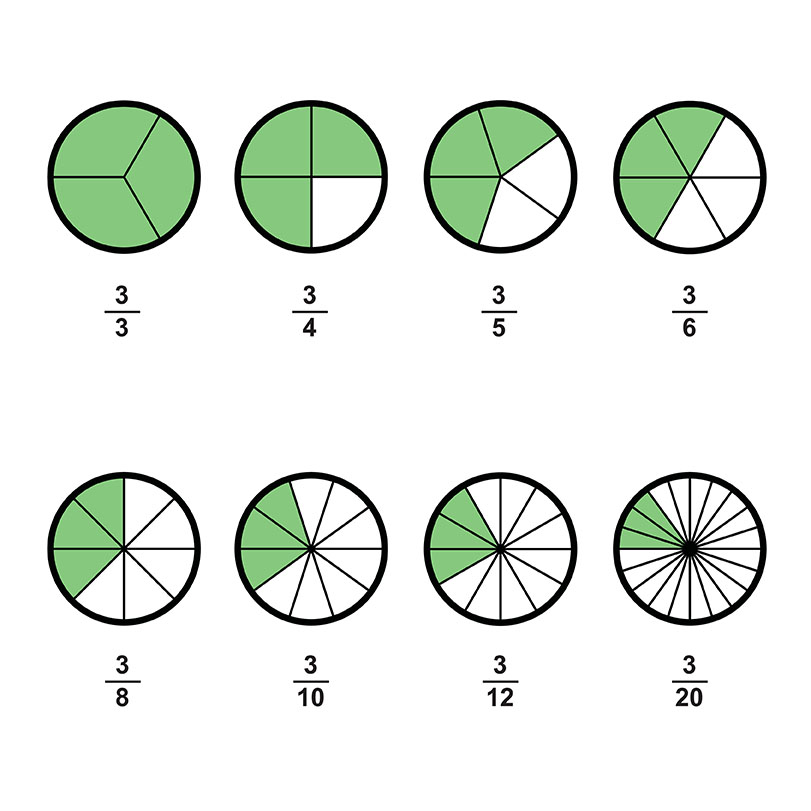
A fraction is a number that represents a part of a whole. It is written as a ratio of two numbers, the numerator and the denominator. The numerator is the number of parts we have, and the denominator is the total number of parts.
For example, the fraction 1/2 means that we have 1 out of 2 parts. We can also write this fraction as 1 divided by 2, or 1/2.
Fractions can be added, subtracted, multiplied, and divided. They can also be simplified, which means that we can write them in a simpler form.
Fractions are a powerful tool for representing and working with parts of a whole. They are used in many different areas of mathematics, including geometry, algebra, and calculus.
How can the word be used?
The fraction 1/3 can be written as 0.33 or 33%.
Different forms of the word
Noun: fraction, fractions.
Adjective: fractional.
Verb: fractionate, fractionated, fractionating.
Etymology
The word "fraction" comes from the Latin word fractus, which means "broken" or "divided". The Latin word fractus is made up of the verb frangere, which means "to break", and the suffix -tus, which indicates a past participle.
Question
What is a fraction?
AQA Science Exam Question and Answer
Question:
Explain the concept of a fraction and its representation in mathematics. Describe the parts of a fraction, including the numerator and denominator, and their significance in denoting a part of a whole or a ratio. Provide real-life examples of how fractions are used in various situations, such as dividing a pizza or calculating probabilities.
Answer:
A fraction represents a part of a whole or a ratio of two quantities in mathematics. It consists of two parts: the numerator, which represents the number of equal parts being considered, and the denominator, which denotes the total number of equal parts that make up the whole.
For example, in the fraction 3/4, the numerator is 3, indicating that there are three parts of the whole, while the denominator is 4, representing that the whole is divided into four equal parts.
Fractions have practical applications in various situations. Dividing a pizza into equal slices, calculating probabilities in statistics, and measuring ingredients in recipes are everyday examples of using fractions.
Understanding fractions is essential in various mathematical concepts, including arithmetic, algebra, and probability, and it is a valuable skill in solving real-life problems involving parts of a whole or comparing quantities.