
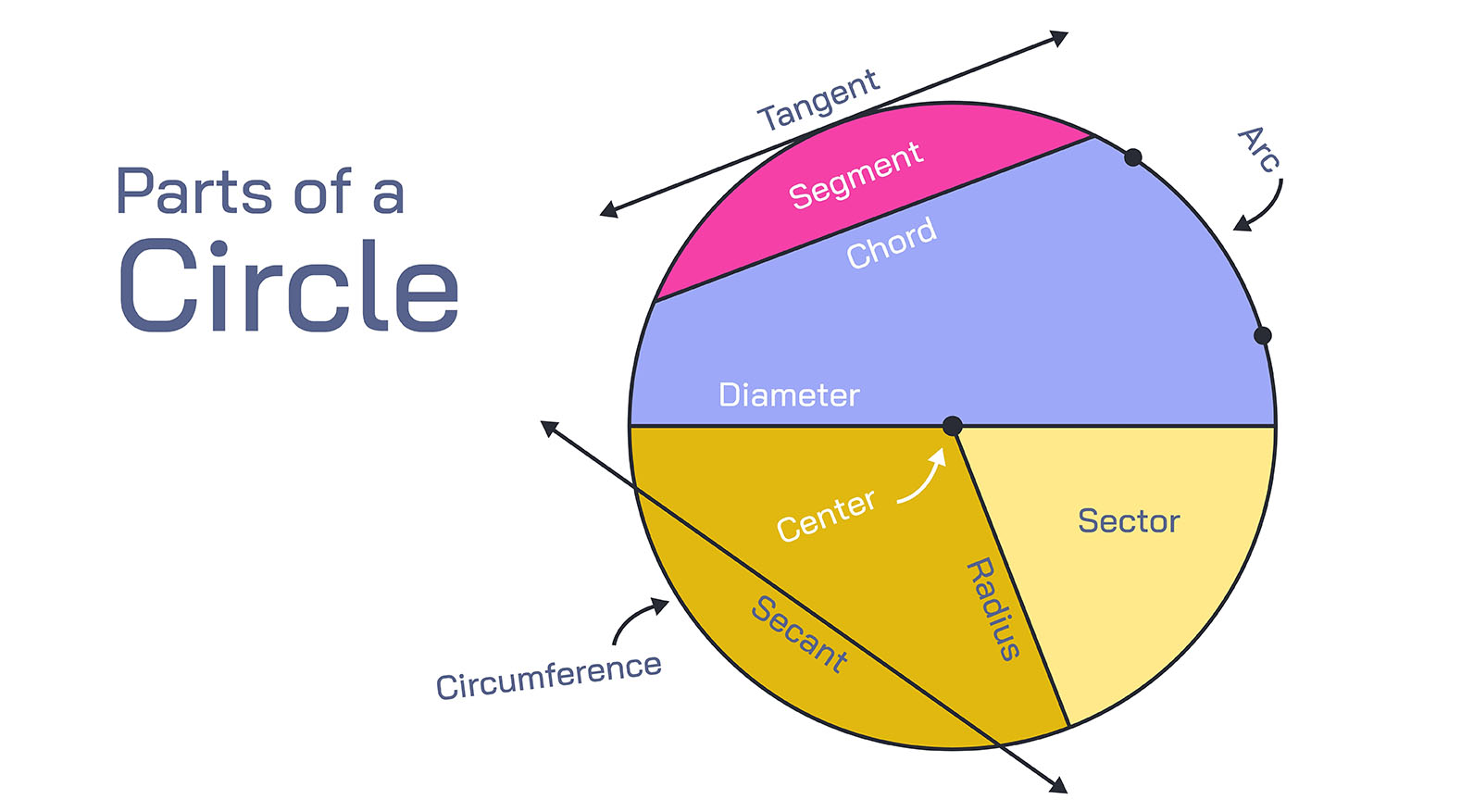
arc
Definition
Arc is a part of a circle. It is a curved line that forms part of the circumference of a circle. An arc is a shorter distance than the full circle, but it still has all the same properties of a circle.
The arc length is the distance along the arc, and the arc measure is the angle that the arc subtends at the centre of the circle. The arc measure is measured in degrees or radians.
Arcs are used in many different ways in science. For example, they are used to measure the size of the Earth, to design bridges, and to make telescopes.
Here are some examples of arcs:
- The rainbow: The rainbow is an arc of light that appears in the sky after it rains.
- The arch of a bridge: The arch of a bridge is an arc that supports the weight of the bridge.
- The lens of a telescope: The lens of a telescope is an arc that focuses light.
- Here are some formulas for arc length and arc measure:
- Arc length = (arc measure) * (radius)
- Arc measure = (arc length) / (radius)
How can the word be used?
The arc lamp was used to light the stage, creating a dramatic effect.
Different forms of the word
Noun: arc.
Adjective: arced, arcing.
Verb: arc, arc over, arc up.
Synonyms: curve, bend, bow, semicircle.
Antonyms: straight line, curve.
Etymology
The word "arc" comes from the Latin word arcus, which means "bow" or "arch." The Latin word is derived from the Proto-Indo-European root arḱ-, which means "to bend.".
Question
What is an arc?
AQA Science Exam Question and Answer
Question:
What is an arc and how is it formed?
Answer:
- An arc is a part of a circle that is less than a full circle. Arcs are formed when a circle is cut by a straight line.
- The length of an arc is measured in degrees. The angle formed by the two end points of the arc and the centre of the circle is called the arc's central angle.
- The ratio of the arc's central angle to 360 degrees is equal to the ratio of the arc's length to the circle's circumference.
- For example, if an arc's central angle is 90 degrees, then the ratio of the arc's length to the circle's circumference is 1/4.
- Arcs are used in many different applications, such as bridges, arches, and rollercoasters.